Algumas forças comuns na natureza
Força peso
É a força com que a Terra atrai os corpos. Quando um corpo está em queda livre aumenta aproximadamente 10 m/s a cada segundo.
Como vimos, a grandeza que mede a variação da velocidade do corpo à medida que o tempo passa é aaceleração. Vimos que a aceleração da gravidade possui valor de:
O valor da aceleração da gravidade não é o mesmo para todos os astros do universo.
Quanto maior o valor da aceleração da gravidade, maior é a força que os planetas exercem para atrair os demais corpos, mais ele será atraído pelos planetas. Portanto, o peso é diretamente proporcional à massa do corpo e à aceleração da gravidade.
Logo, podemos expressar o peso de um corpo P por meio de uma relação matemática, na qual o peso corresponde ao produto da massa (m) do corpo pela aceleração da gravidade no local (g). |
Ou seja:
Uma questão importante é entender qual a diferença entre peso e massa.
Massa é uma propriedade dos corpos relacionada à quantidade de matéria que o corpo possui. A massa não depende do local onde o corpo se encontra. A unidade de medida da massa no Sistema Internacional é o kilograma (Kg).
O peso depende, além da massa, do valor da aceleração da gravidade local, e é uma força cuja unidade no Sistema Internacional é o Newton (N).
Imagine dois corpos idênticos, um na Terra e outro na Lua. Eles têm a mesma massa, mas o corpo que está na Lua, onde a aceleração da gravidade vale 1/6 da aceleração da gravidade terrestre, tem peso 6 vezes menor que o peso do corpo que está na Terra.
Veja um exemplo:
Na Terra, o peso de uma pessoa de 60 kg de massa será: 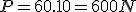
Na Lua, o peso dessa mesma pessoa será : 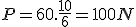
Observe que a frase “Meu peso é 50 Kg!”, apesar de muito comum, está errada. O correto é afirmar: “Minha massa é 50Kg”.
Uma outra unidade bastante comum para medir forças é o quilograma-força (Kgf). Um Kgf é uma força com que a Terra atrai um quilograma, ao nível do mar e a 45º de latitude. Portanto, quando uma pessoa se “pesa”, caso sua massa seja 50 Kg, pode-se afirmar que ela tem 50kgf de peso.
Representamos a força peso no centro da gravidade do corpo, sempre vertical para baixo |
Força normal
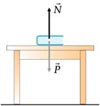
É a força que a superfície de apoio aplica no corpo, e sua direção é sempre perpendicular a esta superfície.
Porque um corpo não cai quando está apoiado em uma mesa? Ele não cai porque a mesa o “segura”.Essa força é chamada força normal, e seu símbolo é 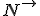
Tração ou tensão
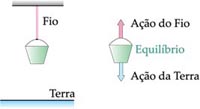
São forças transmitidas por meio de fios. A força de tração, cujo símbolo é 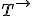 sempre “puxa” o corpo e tem a direção do fio.
sempre “puxa” o corpo e tem a direção do fio.
Como medir forças?
O aparelho mais usado para medir forças é o dinamômetro. O tipo mais comum é o dinamômetro de mola, que possui um gancho em uma das duas extremidades no qual penduramos um objeto. A mola distende e registra o valor da força sobre uma escala numérica.
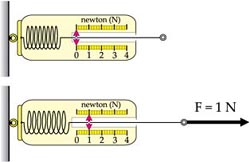
As balanças de farmácia com ponteiro seguem o mesmo princípio dos dinamômetros, porém a mola é comprimida. A pessoa sobe numa plataforma, comprime uma mola, e essa compressão é proporcional ao deslocamento do ponteiro.
Primeira lei de Newton
Imagine um bloco de madeira em repouso sobre uma mesa. Esse bloco tende a permanecer em repouso a menos que “algo” o coloque em movimento.
Esse “algo” é a ação de uma força. Imagine que o bloco seja colocado em movimento com a aplicação momentânea de uma força horizontal. O bloco se move por um certo espaço e pára novamente.
Se o bloco e a mesa forem lixados até ficarem bem lisos, a aplicação da mesma força permitirá que ele se desloque por um, espaço maior antes de parar. Se, finalmente, sobre a mesa for passado óleo lubrificante, então o bloco deslizará por uma distância ainda maior.

Essas evidências nos dão uma indicação de porque o bloco pára. Ele pára graças a sua interação que existe entre sua superfície e a da mesa, proveniente da aspereza das duas superfícies, que raspam uma na outra enquanto o bloco se move. Essa interação é o atrito. Quando as superfícies são lixadas e lubrificadas, o atrito não é totalmente eliminado, mas é bastante reduzido. Outro fator que se opõe à movimentação do bloco é a resistência do ar.
E se fosse possível eliminar completamente a resistência do ar e o atrito, o que aconteceria com o bloco, uma vez colocado em movimento?
A resposta a essa pergunta formulada por Isaac Newton no século XVII, que ainda hoje é considerado pelos cientistas como válida, é que o corpo permaneceria em movimento retilíneo (e linha reta) e uniforme (com velocidade constante), para sempre.
Você achou isso estranho?
A situação de movimento perpétuo não nos parece óbvia porque vivemos em um planeta na qual há pelo menos dois fatores que dificultam a análise dos movimentos: a resistência do ar e o atrito.
Imagine que fosse possível a um astronauta, no espaço distante, estar longe de qualquer corpo celeste. Se ele aplicasse força sobre uma bola para colocá-la em movimento, a bola, livre da resistência do ar e do atrito com outros corpos, continuaria para sempre em movimento retilíneo uniforme.
A primeira lei de Newton, ou princípio da Inércia, pode ser enunciada como:
Um corpo que está em repouso tende a permanecer em repouso, a menos que sobre ele passe a atuar uma força resultante. E um corpo que está em movimento retilíneo e uniforme tende a permanecer em movimento retilíneo uniforme, a menos que sobre ele passe a atuar uma força resultante. |
Que o estado de repouso é uma tendência natural e que ele só é alterado graças à aplicação de uma força é uma afirmação relativamente fácil de aceitar, pois está de acordo com muitas observações cotidianas. A grande inovação da primeira lei de Newton é considerar o movimento retilíneo e uniforme como um estado equivalente ao repouso, e afirmar, portanto, que esse estado também só pode ser alterado mediante a atuação de uma força resultante.
Um corpo sempre oferece resistência a alteração em seu estado de repouso ou de movimento retilíneo e uniforme. Essa resistência é denominada inércia e é uma característica dos corpos. Cada corpo possui uma inércia que lhe é característica e, como veremos mais à frente, a massa do corpo é a medida da inércia desse corpo.

Para ilustrar: quando um carro arranca, os corpos dentro dele são “puxados” para trás. Quando freia, projetados para frente.
Segunda lei de Newton
Força resultante produz aceleração
Se um corpo está em repouso (em relação a um certo referencial), sua velocidade é zero. Se for colocado em movimento, sua velocidade deixará de ser nula e, portanto, o objeto foi acelerado. De modo similar, se um corpo em movimento retilíneo e uniforme (e, portanto com aceleração nula, já que a velocidade é constante) for forçado a parar, também podemos afirmar que ele sofreu uma aceleração (popularmente fala-se, nesse caso, em “desaceleração”).
Primeira Lei de Newton, em ambas as situações – do repouso ao movimento retilíneo e uniforme, ou ao contrário -, uma força resultante atua sobre o corpo.
Disso, concluímos que a atuação de uma força resultante sobre um corpo produz nele uma aceleração.
Esse é o tema da Segunda lei de Newton, que veremos a seguir.
Perceber, por meio de experimentos, a relação entre força e aceleração não é uma tarefa muito fácil, devido às complicações representadas pelo atrito e pela resistência do ar.
Imagine um bloco de massa 1 kg esteja em repouso sobre uma superfície perfeitamente lisa. Submetido à ação de uma força resultante horizontal de intensidade F, esse bloco adquire uma aceleração de 1 m/s2, conforme ilustrado em A. Se a mesma força resultante atuar sobre o bloco de massa 0,5Kg, verifica-se que a aceleração adquirida será de 2 m/s2, conforme B.
Se um força resultante horizontal com dobro da intensidade 2F, atuar num bloco de massa 1kg, ele adquire aceleração de 2m/s2 (veja C), e se atuar num bloco de massa 0,5 kg, ele adquire aceleração de 4 m/s2 (veja D).
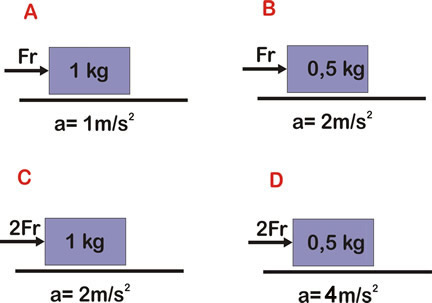
Você percebe a regularidade matemática envolvida?
Analisando o exemplo acima
Comparando A e C, percebemos que, quando a força resultante que atua sobre um certo corpo é duplicada, a aceleração decorrente também duplica. A mesma conclusão pode ser tirada comparando Be D. Muitos experimentos desse tipo permitem fazer a generalização seguinte.
Em palavras: A aceleração de um corpo é diretamente proporcional a força resultante que atua sobre ele.
Comparando B e C, verificamos que, se a massa de um corpo é o dobro da de outro, é necessário que a força resultante seja duplicada, para acelerá-lo igualmente. Vários experimentos como esse levam à conclusão a seguir.
Em palavras: A força resultante que produz certa aceleração num corpo é diretamente proporcional a sua massa.
Finalmente, comparando A e B, verificamos que, se dois corpos estão submetidos à mesma força resultante e se um deles tem metade da massa do outro, então esse adquirirá o dobro da aceleração. A mesma conclusão pode ser tirada comparando C e D. Isso pode ser generalizado como segue.
Em palavras: Sob a ação de uma força resultante, a aceleração de um corpo é inversamente proporcional à sua massa.
Agora considere a equação e sua simbologia:
Fr – módulo de força resultante que atua sobre um corpo
m – massa do corpo
a – aceleração do corpo
podemos enunciar matematicamente as conclusões tiradas acima.
Em equação: |
Essa equação matemática foi enunciada por Isaac Newton no século XVII e é conhecida como segunda Lei de Newton, ou Princípio fundamental da Dinâmica.
A unidade kg.m/s2, que aparece nesse cálculo, pode ser usada para expressar a intensidade (módulo) de uma força. É simplificadamente denominada Newton e representada por N.
Assim, podemos afirmar que um Newton (1N) é a intencidade de uma força resultante que, atuando em um corpo de massa 1kg, faça com que ele adquira a aceleração de 1m/s2.
A força resultante que atua sobre o corpo nos casos A e B do exemplo acima tem intensidade 1N.
Retomando o exemplo, observe que nos quatro casos (A, B, C e D), é obedecida a equação
A 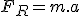
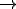
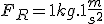
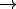
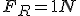
B 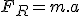
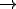
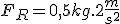
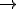
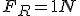
C 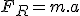
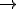
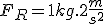
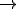
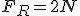
D 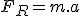
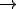
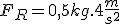
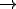
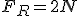
A segunda lei de Newton permite-nos fazer uma série de previsões referentes ao movimento dos corpos. Vamos supor por exemplo, que se deseje fazer com que um corpo de massa 3 kg adiquira a aceleração de 5m/s2. Qual é a força resultante que se deve ser aplicada a esse corpo?
O calculo é o seguinte:
Terceira lei de Newton
Se um martelo em queda atingir o seu pé, ele irá machucá-lo por que, no momento do contato, exercerá sobre seu pé uma força. Isso é fácil de entender e de aceitar.
Acontece que seu pé também aplica no martelo uma força com intensidade igual à da força que recebe do martelo. Isso já é mais difícil de entender e de aceitar.
Vamos, então, escolher um exemplo mais convincente. Imagine um ovo caindo no chão. No momento do contato, o ovo aplica sobre o chão uma força vertical para baixo e o chão aplica sobre o ovo uma força vertical para cima, de mesma intensidade. É essa força que faz o ovo quebrar!
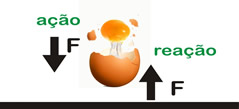
Quando você chuta uma bola, aplica a ela uma força que a faz movimentar-se. Simultaneamente ela aplica ao seu pé uma força, que você pode sentir. Ao bater com a mão numa parede, você estará aplicando uma força a ela. Ao mesmo tempo, sua mão receberá da parede uma força de mesma intensidade, que poderá até machucá-la.
Newton expressou idéias como essas por meio da chamada Terceira Lei de Newton, ou princípio da ação e reação, que pode ser enunciada como segue.
Para qualquer força que um corpo A aplique a um corpo B, haverá uma força de mesma intensidade, de mesma direção, mas de sentido contrário, aplicada pelo corpo B ao corpo A. Um dessas duas forças, não importa qual, pode ser chamada ação e a outra, reação. |
Ação e reação atuam em corpos distintos
A terceira lei de Newton revela uma importante característica das forças: elas sempre ocorrem aos pares. Em outras palavras, forças são o resultado da interação entre os corpos. É o martelo interagindo com o pé, o ovo interagindo com o chão, a mão interagindo com a parede etc.
Uma característica muito importante de todo o par de forças ação-reação é que elas atuam em corpos distintos, nunca no mesmo corpo. Quando alguém tenta empurrar a parede (a palavra “empurrar” indica aqui uma aplicação de uma força e não um movimento), a parede empurra essa pessoa com força de mesma intensidade e mesma direção mas sentido oposto. Uma dessas forças, aquela aplicada pela parede, age sobre a pessoa.
Já que ação e reação atuam sobre corpos distintos, elas freqüentemente têm efeitos distintos. Quando uma bola de futebol atinge uma vidraça, ambos os corpos interagem; a força que a vidraça aplica à bola reduz sua velocidade, enquanto a força que a bola aplica à vidraça pode quebrá-la.
A força de atrito
Agora pense! Quando uma criança empurra um carrinho de brinquedo no chão, por que ele pára? Ele deveria continuar em movimento para sempre?

A resposta é não! O carrinho somente continuaria em movimento retilíneo uniforme para sempre caso a resultante das forças que atuassem nele fosse nula. Mas não é. Há uma força que o chão exerce no corpo, paralela ao chão e contrária ao movimento. Essa força é chamada de força de atrito.
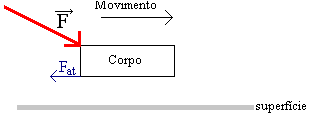
A força de atrito depende da textura das superfícies que estão em contato. Quanto mais polida, menos resistência uma superfície oferece ao movimento de um corpo que se desloca sobre ela.

Essa força de atrito também depende da força que o corpo em movimento faz perpendicularmente à superfície. Quanto maior essa força, maior a força de atrito.
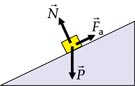
Às vezes, a forças de atrito atua no corpo sem que ele esteja em movimento. Por exemplo, um corpo fica em repouso sobre um plano inclinado porque a força de atrito está impedindo que esse corpo deslize pelo plano. A força de atrito é sempre contrária à tendência de movimento do corpo.
Newton e a gravitação
Um pequeno automóvel de brinquedo, movido a pilha e que anda em linha reta, foi amarrado a uma linha. A outra extremidade da linha foi amarrado a um anel de metal e este foi encaixado num prego fixado ao centro de uma tábua.
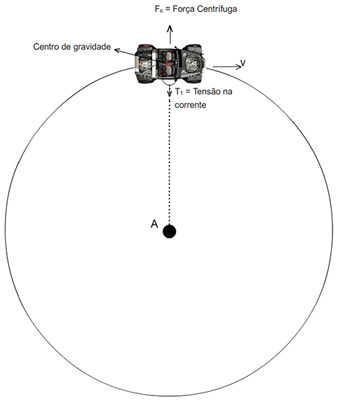
Quando o automóvel foi ligado, verificou-se que, em vez de seguir em linha reta, realizou commovimento circular.
Como explicar cientificamente por que o fio impede o movimento em linha reta?
Conceito da força centrípeta
Analisando o resultado do experimento
A tendência de o automóvel de brinquedo mover-se em linha reta faz a linha esticar. Isso origina umaforça de tração na linha. Essa força, ao agir sobre o brinquedo, o impede de prosseguir em linha reta na mesma direção.
Em todos os pontos de sua trajetória circular acontece exatamente o mesmo: o brinquedo tende a seguir em linha reta, mas a força de tração impede que isso aconteça, modificando continuamente a direção do movimento e produzindo a trajetória circular.
Se, num dado instante, a linha subitamente se arrebentar ou for cortada, o automóvel imediatamente deixará a trajetória circular e prosseguirá em linha reta. Em outras palavras, a partir do momento em que a força de tração deixar de atuar, o brinquedo automaticamente abandonará o movimento circular e sairá pela reta tangente à circunferência.
A força de tração no fio é chamada força centrípeta. A força centrípeta atua sobre todo móvel que descreva uma trajetória curva, seja uma circunferência ou qualquer outro tipo de curva. Essa força é responsável pelo fato de o movimento não ser retilíneo e sim curvilíneo. A direção da força centrípeta passa pelo móvel e pelo centro da curva descrita por esse móvel. E o sentido da força centrípeta aponta para o centro dessa curva.
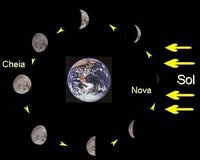
Esse tipo de força ocorre, por exemplo, no movimento da Lua em torno da Terra. A força com que a Terra atrai a Lua atua de modo que esta última mude a direção do seu movimento a cada instante, mantendo o seu movimento em torno da Terra em trajetória curva.
Máquinas simples, trabalho e energia
Em nosso dia-a-dia, vivemos cercados de máquinas. É muito comum nos depararmos com máquinas de todos os tipos, desde as mais simples até as mais complexas. Usamos um abridor para abrir latas, cortamos papel com uma tesoura, penduramos quadros em pregos fixados na parede pelos martelos e seguramos as crianças pequenas em carrinhos de bebê.
Somos cada vez mais dependentes de máquinas cada vez mais complexas, como os carros ônibus e os trens que utilizamos para ir a escola, ao local de trabalho etc.
Maquinas simples
Sabemos que as máquinas variam das mais simples as mais complexas. Máquinas complexas são aquelas que utilizam dispositivos eletrônicos em sua composição, como os circuitos integrados. Um exemplo de máquina complexa são os computadores.

Automóveis utilizam também recursos eletrônicos e elétricos, mas seu funcionamento se baseia principalmente em peças se deslocando: puxando, empurrando, girando etc.; enfim, são peças se movendo. Esse tipo de funcionamento, portanto, é do domínio da mecânica.
Toda máquina tem uma ou várias funções. Iremos iniciar o estudo de algumas maquinas que facilitam a atividade humana simplesmente por nos permitir realizar uma tarefa com menor esforço físico. Por exemplo, quando pregamos um prego na parede com um martelo, fazemos um esforço muito menor do que o necessário para pregá-lo usando apenas as mãos, o que certamente nem conseguiríamos.

Denominaremos de máquinas simples às que modificam e transmitem a ação de uma força para realizar algum movimento. Abridor de latas, martelo, tesoura, chave de fenda, alicate, quebra-nozes, carrinho de mão, pinça e cortador de unha são exemplos de máquinas simples.
Maquinas simples são aquelas que modificam e transmitem a ação de uma força para realizar algum movimento.
Alavancas
Imagine a seguinte situação: você precisa levantar um saco cheio de mantimentos. A massa total do saco é 120 kg. Poucas pessoas conseguem, e geralmente somente aquelas que se preparam para isso. Entretanto, no decorrer da história, as pessoas muitas vezes tiveram que levantar pedras ou objetos, e não contavam com máquinas para auxiliá-las. Há mais de 22 séculos, um homem chamadoArquimedes (287 – 212 a.C.) encontrou um método extremamente simples para resolver esse problema: ele descobriu as alavancas.
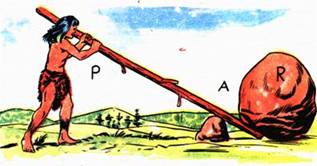
Uma alavanca nada mais é do que uma barra rígida que pode girar em torno de um ponto de apoio.
Em pleno século III a.C. Arquimedes afirmou: “Dê-me uma alavanca que moverei o mundo”
Como você poderia, com auxilio de uma alavanca, levantar um saco de 120 kg, fazendo uma força equivalente à que faria para levantar um saco de 20kg de arroz? Em outras palavras, como levantar uma massa com peso seis vezes maior que outra, fazendo a mesma força que faria para levantar essa?
Simples! É só a distância entre o ponto da barra rígida em que você aplica a força e o ponto de apoio (de P a A) ser seis vezes maior do que distância da massa até o ponto de apoio (de A a R).
Vamos denominar:
- Força resistente – é a força que queremos equilibrar. No exemplo acima, é o peso do saco de mantimentos.
- Força potente – é a força que sustentará a resistência. No exemplo, é a força que fazemos.
Tipos de alavancas
INTER-FIXA: É quando o ponto apoio (A) está entre a aplicação da força potente (P) e a aplicação da força resistente (R). | INTER-PONTENTE: É quando a aplicação da força potente (P) está entre a aplicação da força resistente (R) e o ponto de apoio (A). |
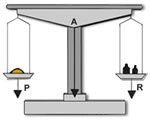 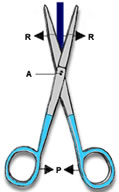 | 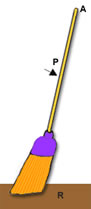 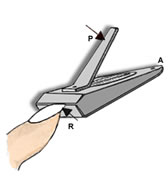 |
INTER-RESISTENTE: É quando a aplicação da força resistente (R) está entre a aplicação da força potente (P) e o ponto de apoio (A). |
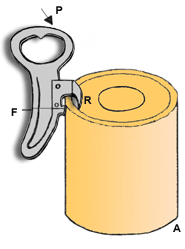 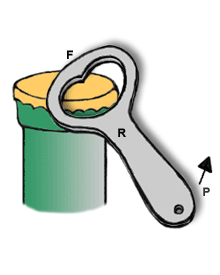 |
Equação das alavancas
Pediremos ajuda a matemática para encontrar uma expressão para a seguinte situação.
Equilibrar uma massa muito grande fazendo uma força bem menor que o peso dessa massa que queremos sustentar.
Vamos denominar:
R: valor da força resistente – a força que queremos equilibrar.
P: valor da força potente – é a força que sustentará a resistência.
BR: braço de resistência – é a distância do centro de gravidade do corpo ao ponto de apoio.
BP: braço de potência – é a distância do ponto de aplicação da força ao ponto de apoio.
O: Ponto de apoio
Verificamos que o equilíbrio será alcançado quando:
Exemplo de aplicação
Vamos calcular a força que um pedreiro tem de fazer para carregar 80 kg de terra com a ajuda de um carrinho de mão que possui 1,80 metros de comprimento. Sabendo que a distância entre o centro de gravidade do volume de terra até o centro da roda do carrinho é 90 cm.
Primeiramente vamos verificar qual tipo de alavanca temos.
Como o que fica no meio do carrinho é a terra, ou seja, a resistência, a alavanca é inter-resistente.
Temos:
braço de resistência = 90 cm = 0,9 m
braço de potência = 1,80 m
resistência = 80 kgf.
Portanto,
A interpretação física desse cálculo é a seguinte: o pedreiro necessita fazer uma força com intensidade de metade do peso do volume de terra para erguer o carrinho e transportar a carga.
Você percebeu a grande utilidade de uma máquina tão simples?
Roldanas e polias
Você já observou pessoalmente, em programas esportivos ou em filmes, que nas academias de ginástica os aparelhos de musculação são cheios de discos rígidos em torno dos quais há um fio, em que estão presas as cargas? Para que servem?

Esses discos são denominados roldanas ou polias. São discos com um canal por meio do qual passa um fio ou corda, em que está presa uma carga.
Roldanas fixas
A roldana fixa facilita a realização de um esforço por mudar a direção da força que seria necessária. Nesse caso, como observamos na figura, a força necessária para equilibrar o corpo é igual à força realizada pela pessoa. Entretanto, para levantar a carga, temos que puxar para baixo, o que facilita o trabalho.
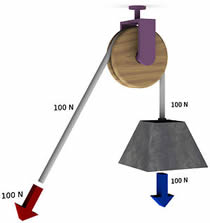
Roldanas móveis
As roldanas móveis diminuem a intensidade do esforço necessário para sustentar um corpo, pois parte desse esforço é feito pelo teto, que sustenta o conjunto.
Observe na figura a baixo, como a roldana móvel pode facilitar o trabalho.
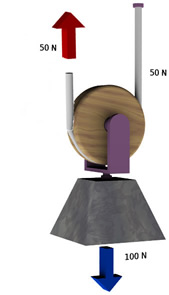
- Com uma roldana móvel, a força necessária para equilibrar a carga é dividida por dois (21).
- Com duas roldanas móveis, a força necessária é dividida por quatro (22).
- Com três, é dividida por oito (23), e assim sucessivamente.
Agora já sabemos a razão de haver tantas polias em uma sala de musculação. Elas tornaram viáveis o esforço que queremos realizar, em geral mudando de direção da força necessária para levantar os pesos, a fim de trabalhar a musculatura desejada.
O plano inclinadoImagine que você está carregando um monte de livros e tem de levá-los para uma sala localizada em um andar acima do andar em que está.
Para isso, você poderá optar por utilizar uma de duas rampas. A primeira é bem inclinada, e a outra tem inclinação suave.
Qual rampa você escolheria? Bem, se quisesse fazer menos esforço, provavelmente você não teria dúvidas em escolher a mais suave. Planos inclinados facilitam muito o levantamento de pesos. Quanto menor a inclinação, menor a força.

O conceito de Trabalho
Imagine que você esteja levantando um livro ou empurrando uma mesa ou um carrinho de bebê. Em todas essas atividades está realizando trabalho. Também realiza trabalho quando produz um texto, atende o telefone ou lava as louças do almoço.

Entretanto, o conceito de Trabalho em Física é um pouco diferente do conceito que atribuímos a essa palavra em nosso cotidiano. Em física, diz-se que um trabalho foi realizado quando uma força foi usada para deslocar um corpo. Nesse caso, o trabalho é proporcional à força que desloca o corpo e ao deslocamento produzido por ela, ou seja, quanto maior a força, maior será o trabalho, equanto maior o deslocamento, também maior será o trabalho.
O conceito do Trabalho, em física, foi criado em plena Revolução Industrial, quando a humanidade iniciou a produção de máquinas mais complexas, que permitiram o desenvolvimento industrial de algumas nações do planeta.
Portanto, se a força atuar na direção e sentido do deslocamento, podemos definir matematicamente o conceito de Trabalho, cujo símbolo é t, lê-se: tau.
Nessa expressão matemática, F é a força e d é o deslocamento.
A unidade de trabalho no Sistema Internacional é o N.m, que denominamos de Joule (J).
Essa definição só vale quando a força atua na direção e no sentido do deslocamento e tem seu valor constante. Por exemplo, quando pressionamos um corpo contra uma mesa, estamos fazendo força, mas essa força não contribui em nada para deslocar o corpo. Portanto, não realiza Trabalho.
Por exemplo, para empurrar uma mesa por meio metro, fazendo uma força de 10N paralela à mesa, realizamos um Trabalho que pode ser calculado desse modo:
O Trabalho de uma força paralela e no sentido do deslocamento é o produto da força por esse deslocamento.
O trabalho da força peso
O trabalho da força peso 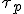 é o valor do peso multiplicado pela variação na altura e na elevação de um corpo.
é o valor do peso multiplicado pela variação na altura e na elevação de um corpo.
Onde: P é o peso do corpo;
m é a massa do corpo;
g é a aceleração da gravidade local;
h é a variação de altura que o corpo sofreu.
Nenhum comentário:
Postar um comentário